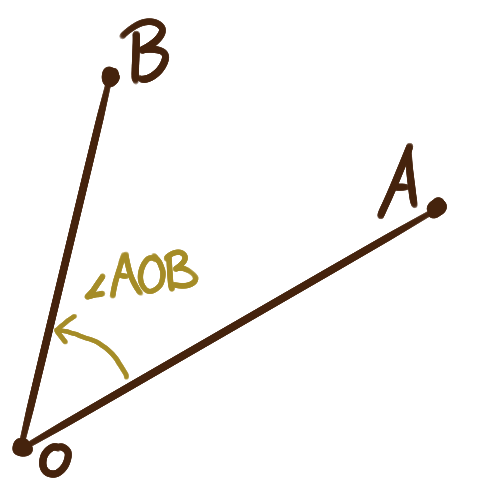Given an “origin” point \(O,\) and two other points \(A\) and \(B,\)
the angle \(\angle AOB\) is the rotation
from the initial side \(\overrightarrow{OA}\)
to the terminal side \(\overrightarrow{OB}.\)
The measure of an angle is the “magnitude” of that rotation.
Conventionally, angles swept out counterclockwise are positive
and angles swept out clockwise are negative.
Two angles are coterminal
if their initial and terminal sides coincide;
they differ only by a number of full rotations.
An angle’s principal angle is the smallest positive angle
— less than a full rotation —
to which it is coterminal.
There are multiple ways to measure angles. One convention is to declare one full rotation to be 360 degrees (°) and measure an angle by how many degrees it spans. When measuring in degrees there are two conventions for representing fractions of a degree: either literally as a decimal number of degrees, or in terms of minutes (′) and seconds (″) where 1° equals 60′, and 1′ equals 60″. E.g. 12.58222° ≈ 12°34′56″.
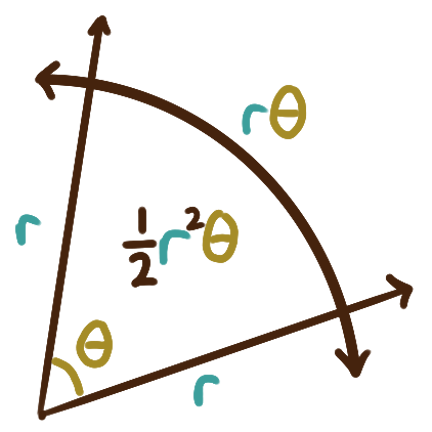Another convention, radian measure,
requires you to first realize an angle
as defining a sector (slice) of some circle of radius \(r.\)
The arc of the sector, the curved boundary of the sector
belonging to the circumference of the circle,
is said to subtend the angle.
The radius and the length of the arc will be directly proportional,
with that proportion depending on \(\theta.\)
We define the radian measure of \(\theta\)
to be this coefficient or proportionality.
I.e. the radian measure of an angle is the number of radius-lengths
required to cover the length of the arc of the sector.
While one full rotation corresponds to an angle with radian measure \(2\pi,\)
the length of just the arc subtending the angle will be \(r\theta,\)
and the area of the sector will be \(\frac{1}{2}r^2\theta.\)
Two angles \(\theta\) and \(\varphi\) are complementary if \(\theta + \varphi = 90°;\) the two non-right angles in a right triangle are complements. Two angles \(\theta\) and \(\varphi\) are supplementary if \(\theta + \varphi = 180°,\) if they together they form a half-rotation, i.e. lie along a straight line.