- Without appealing to technology, describe how the graph of \(g(x) = \sqrt{x-1}+3\) compares to the graph of \(f(x) = \sqrt{x}.\)
- Let \(\gamma(x) = x^{3/2}\) and consider its graph \(y = \gamma(x).\) Suppose we want to shift this graph five to the left; how would the formula for \(\gamma\) have to change to cause this transformation of the graph?
-
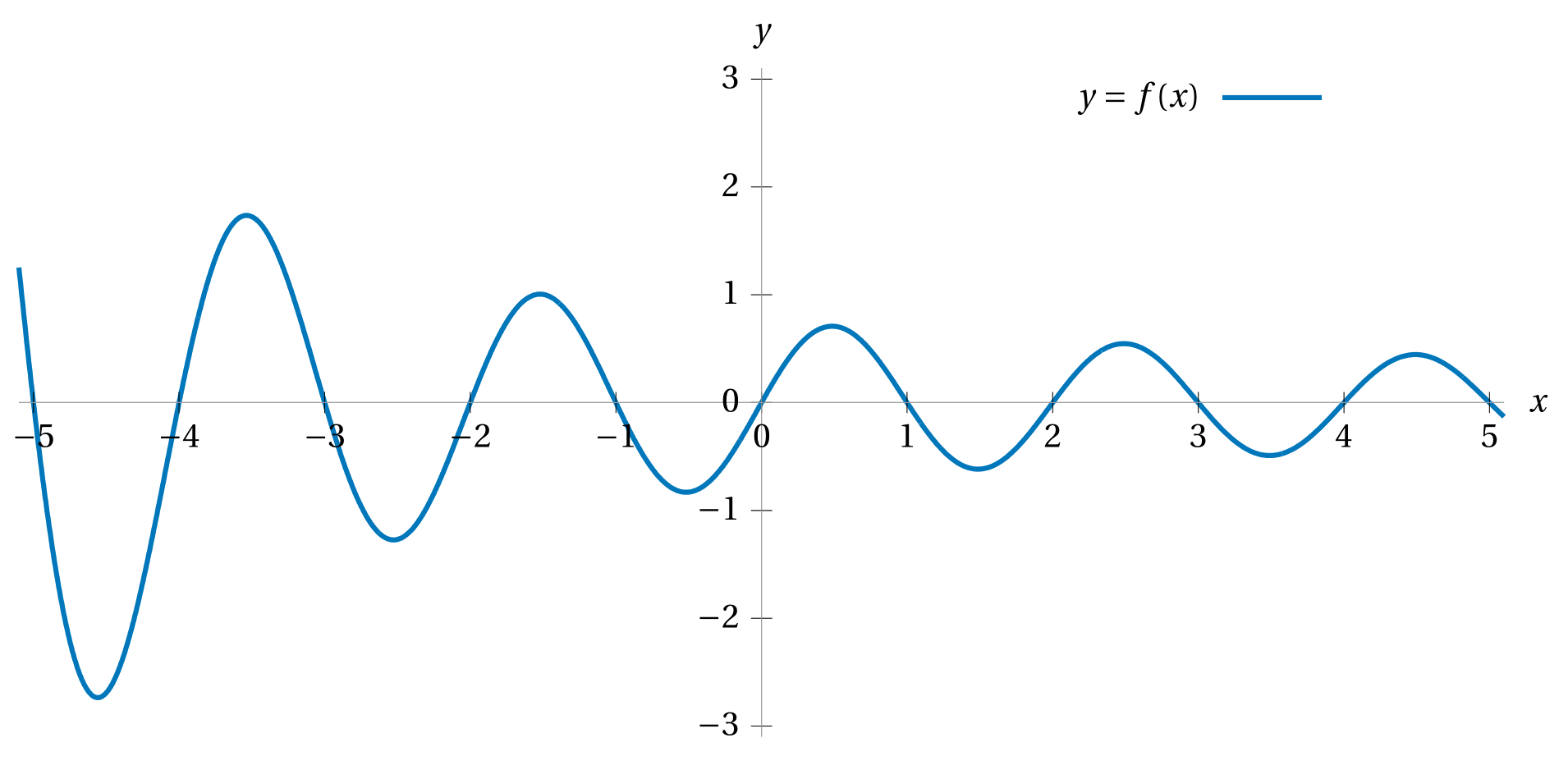
Below is the graph of some function \(f(x).\)
Based on this graph, sketch the graph
of each of the following three functions
on the same set of axes.
\(\displaystyle y = f(x) - 2 \)\(\displaystyle y = 2f(x) \)\(\displaystyle y = f\biggl(x+\frac{3}{2}\biggr) \)
-
For these definitions
of functions \(f\) and \(g,\)
either write out concise formulas for each
of the following new functions,
or evaluate the new function as indicated.
\[
f(x) = x^2-4x
\qquad \qquad \qquad
g(x) = \frac{2}{x}
\]
\(\bigl(f+g\bigr)(x)\)\(\bigl(f-g\bigr)(x)\)\(\bigl(fg\bigr)(x)\)\(\left(3g-\frac{1}{2}f\right)(x)\)\(f\left(-3x\right)\)\(f\left(x+11\right)\)\(\left(f/g\right)(x)\)\(\bigl(f\circ g\bigr)(x)\)\(\bigl(g\circ f\bigr)(x)\)\(\left(f/g\right)(3)\)\(\bigl(f\circ g\bigr)(3)\)\(\bigl(g\circ f\bigr)(3)\)